We return to the faucet and bucket analogy, representing the photodiode of the pixel as the faucet and the depletion region as the bucket. When light falls on a photodiode it creates a flow of photoelectrons which are collected in the bucket. An “exposure” represents the time for which the photoelectrons are collected in the bucket. An image is formed by measuring the number of photoelectrons in each bucket and forming a digital representation of the entire array.
If a static scene is imaged in a sequence of frames, one would expect the value of a pixel to be constant from frame to frame. This however is not the case in the real world. We observe a temporal variation in pixel values, and this is called temporal noise. Under certain conditions, there may also be spatial variations – these are called spatial noise.
Noise in an imaging system is analogous to noise in an audio system, such as that of a poorly tuned radio station. One can consider the audio content as the foreground “signal” of a singer but there may be an interfering audio in the form of a hiss and/or other snaps, crackles and pops that might interfere with our ability to discern the singer’s voice.
In imaging the pristine image is the signal that we are looking to form, and noise is anything that temporally or spatially interferes with our ability to discern it. When forming an image using an image sensor there are several sources of noise.
The first source of noise is the light itself! We may perceive that light in a static scene as being invariant. But light may be modeled as a flow of photons. The number of photons that fall on a given area (such as a pixel) is known to have a statistical variation from one time period to the next. Specifying that a static scene can be modeled as a mean value of 100 photons that are incident on a pixel a in one second, implies that 100 photons is the most likely number of photons that arrive in each second. The actual number of photons that arrive in each second can vary over a range, perhaps from 100 +/- 5 photons with decreasing probability at the numbers furthest away from the mean value of 100 photons.
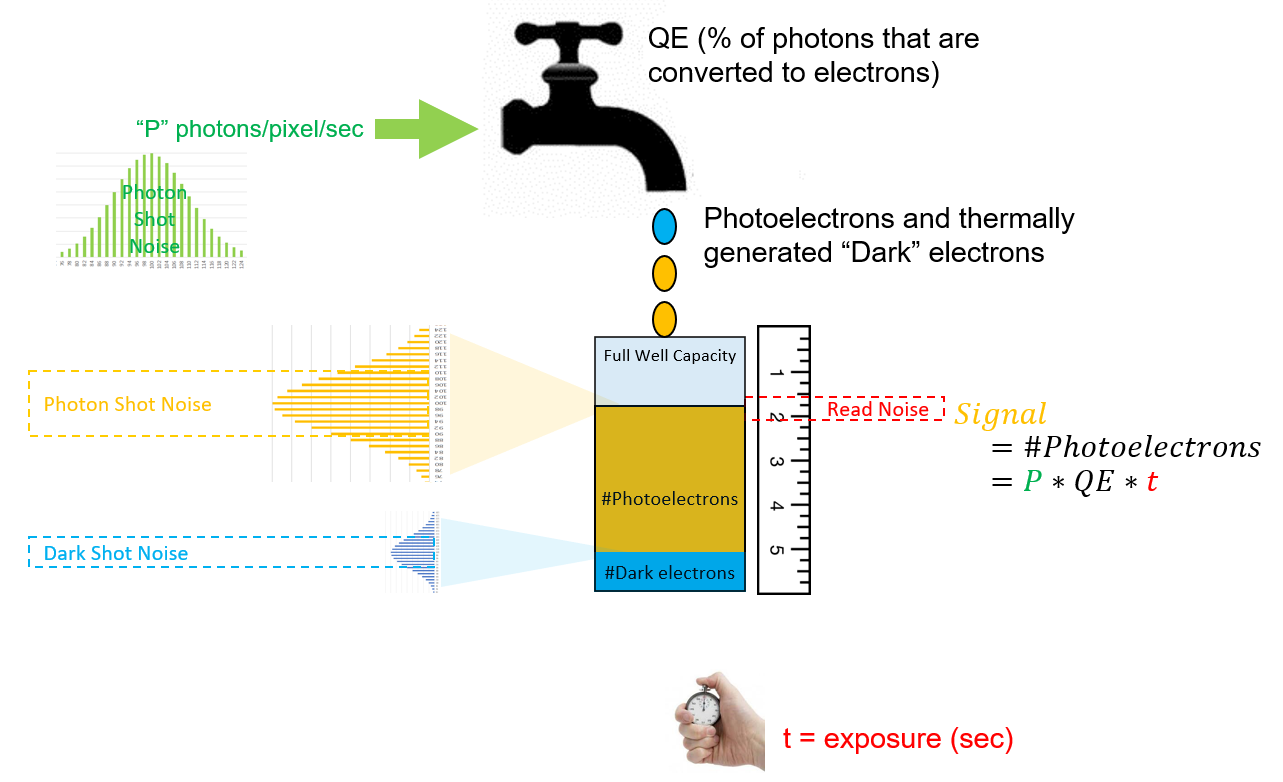
This is inherent in light itself, and one might say that light is accompanied by its own noise source which – unlike the model of a “pure” system – introduces signal AND noise as inputs to the system. Even though the light in the field-of-view (FOV) is static, if the number of photons that fall on a pixel area is measured repeatedly with a perfect measuring instrument there would still be a temporal variation in the value that is observed. This temporal variation is called photon shot noise and, as described above, it is governed entirely by the nature of light itself. This variation is typically modeled as a Poisson distribution, a statistical model that applies to many naturally occurring phenomena in which a previous occurrence does not affect subsequent occurrences. From our knowledge of such distributions we infer that the photon shot noise observed in a pixel is the square root of the number of photoelectrons in a pixel.
Read noise is a term used to describe the temporal variation caused by non-idealities in the measurement process. Although it is typically specified as a number of electrons (for example, read noise = 2e–), it is an aggregate of several different non-idealities. It includes the temporal variations introduced in the process of transferring charges from each pixel, converting charges to a voltage waveform and then digitizing the waveform. Some of these factors are dependent upon the imager, but it is also a function of the design, partitioning and layout of the camera electronics. For this reason, different cameras that use the same imager may have different values for their read noise. The temporal variation represented by “read noise” is a function of the imager used, the clock rate and the level of care taken by the camera designer to protect the signal from interference.
Dark short noise refers to the fact that even if there is no light at all falling on a pixel, the photodiode “faucet” still has a small flow of “leakage” electrons that are generated thermally. In the article titled The Photoelectric Effect in Image sensors, the energy from a photon was shown to create an mobile photoelectron. Thermal energy can also cause mobile electrons to be generated. Thermally generated electrons are not photoelectrons, but they too collect in the depletion region “bucket”. The flow of thermally generated electrons is called dark current because such electrons flow even when there is no light. Dark current is specified in terms of electrons-per-second (e–/p/s) for each pixel. When the charge accumulated in a pixel is read out there is no way to tell thermally generated “leakage electrons” apart from photoelectrons. Therefore, this dark current adds uncertainty in the total number of electrons that are measured. At longer exposures, dark current can fill up more of the full-well-capacity of the “bucket” thereby reducing the available space for photoelectrons. In addition, the is a temporal variation in the number of dark electrons collected from one exposure to the next. This temporal variation is referred to as dark-shot-noise. Since it also can be modeled as a Poisson distribution, the dark-shot-noise is estimated to be the square root of the number of dark signal electrons that are expected to be captured in each exposure.
In the next topic, we introduce the term signal-to-noise ratio (SNR) as a useful figure of merit for image quality. After considering a few examples of images with different amounts of noise, we will form a quantitative model for the signal and the sources of noise that were described here in qualitative terms.

