Optical Resolution is defined as the smallest sized feature that a given optical system is able to resolve. Resolution is tied to contrast – the ability of the system to discern shades of gray. For the sake of simplicity, the topic of the Optical Resolution in this article is discussed independent of contrast, with the topic of Modulation Transfer Function (MTF) covered in a separate article.
Cameras and lenses contribute in different ways to the overall Optical Resolution of a Camera + Lens system. The lower of the two typically sets the Optical Resolution of the system. Because of this, the Optical Resolution of the overall system may be said to be camera-limited or lens-limited.
Although this is not always true, cameras tend to be more expensive than lenses – therefore, the goal of most system designers is to select a camera first based on the “photonics” requirements, and then select a lens with an Optical Resolution that is better than or equal to the Optical Resolution of the camera.
How is Optical Resolution of a Lens specified?
Lens manufacturers typically provide this number as a specification of the optical quality of the lens. It is normally specified in line pairs per millimeter and it is a function of the optical quality of the lens, including the lens design (including the manufacturing tolerances) and the materials, which contribute to the overall Optical Resolution of the lens.
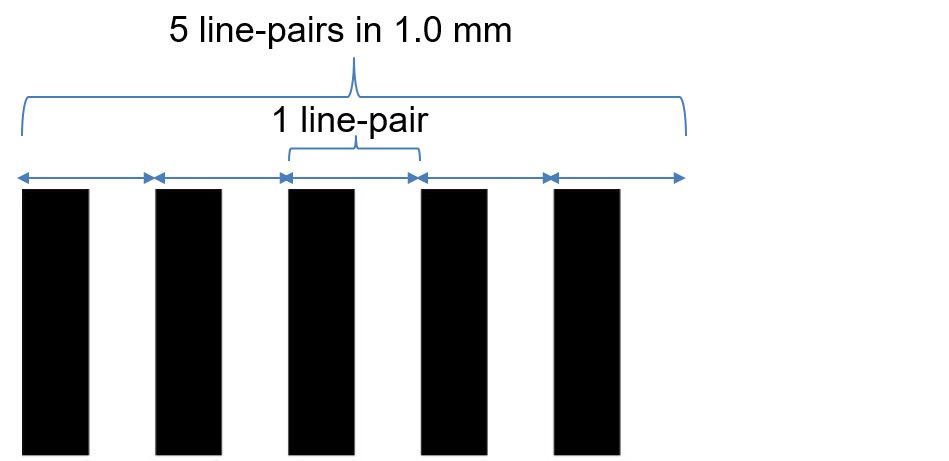
A line pair: 1 black line + 1 white line, each 100μm
Note also that the optical resolution of the lens in lp/mm may be specified with two different numbers representing the optical resolution at the Central | Peripheral regions of the lens. For example, lenses in the 1-1955x series are specified to have Center | Edge resolutions of 100 | 160 lp/mm respectively. This constrains the lens manufacturer to ensure a higher optical quality in the center of the imaging area which tends to be more important to users. Permitting a slightly lower resolution towards the edge allows the lens manufacturer to produce more cost-effective lenses.
If a lens is said to be able to resolve 100 lines per millimeter, it means that the lens can resolve up to 100 equally-sized lines that are small enough to fit within a space of 1mm; for this, each line must be 0.01mm wide. This translates to an optical resolution limit of 10 μm for the system, unless limited by something else (e.g. the size of the pixels).
How does the pixel size of the camera impact the Optical Resolution of the System?
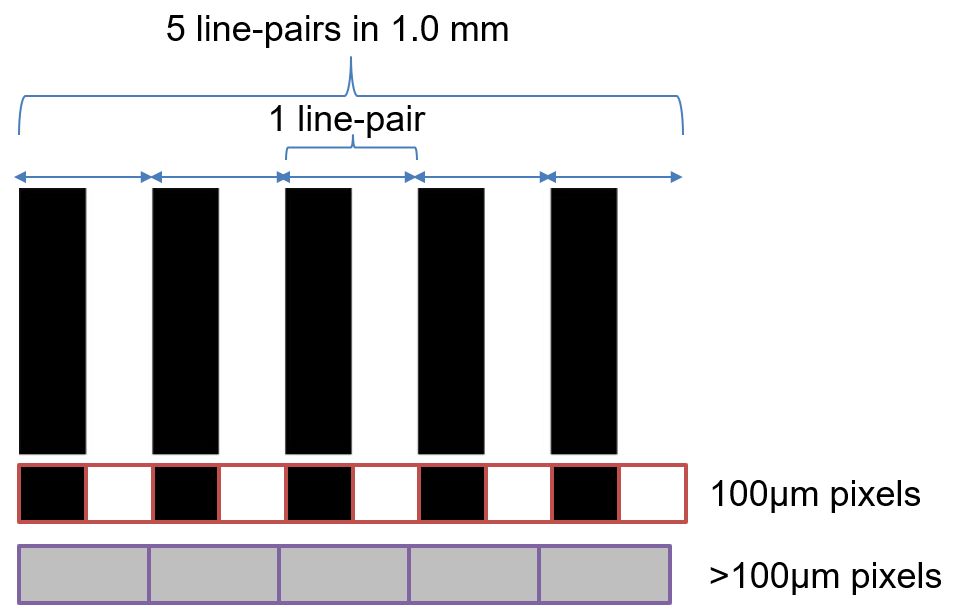
The limiting resolution of a camera with 100μm pixels
= 1000μm/mm ÷ 2 x Pixel Size (in μm)
= 500/Pixel Size (in μm) = 500/100 = 5lp/mm
Per Nyquist, it takes a minimum of two pixels to resolve a feature in an image. The highest spatial frequency which can be resolved by a sensor, the Nyquist frequency, is effectively two pixels or one line pair. One can therefore arrive at a simple formula to estimate the camera-pixel-size limited spatial resolution of a camera:
1mm = 1000μm
Camera pixel size limited resolution (in lp/mm) = 1000/(2 x pixel-size-in-μm) = 500/(pixel-size-in-μm).
For example, a camera that is based on Sony CMOS Pregius Gen2 imagers such as the IMX264 or IMX304 with a pixel size of 3.45μm has the capability of resolving 500/3.45 = 145 lp/mm.
Nyquist limited resolution for different pixel sizes
| Image Sensor type | Pixel Size (μm) | Nyquist Limited resolution (lp/mm) |
| Sony Starvis BSI | 2.4 | 208.3 |
| Sony Pregius Gen1 | 5.86 | 85.3 |
| Sony Pregius Gen2 | 3.45 | 144.9 |
| Sony Pregius Gen3 | 4.5 | 111.1 |
| Sony Pregius Gen4 | 2.74 | 182.5 |
| Sony SenSWIR | 5.0 | 100 |
| sCMOS_6.5μm | 6.5 | 76.9 |
| sCMOS_2.5μm | 2.5 | 200 |
System Considerations
In general, one should consider using a lens that has a higher optical resolution than the camera pixel-size limited resolution. In the above example of a camera with a Sony CMOS Pregius Gen2 imager with 3.45μm pixels, a lens from the 1-1955x series with an optical resolution of 200 lp/mm at the center and 160 lp/mm at the edge would provide a higher system optical resolution since it is not limited by the lens, but by the camera pixel size.
If such a camera is used with the lens that was previously described as being able to resolve 100 lp/mm, the system will be limited by the lens and not the camera. This means that a camera that was capable of an optical resolution of 145 lp/mm is lens-limited to an optical resolution of 100 lp/mm.
Note that lenses with lower optical resolution can be used if optical resolution is not a paramount concern, and cost-effective, lower resolution lenses are quite usable in such applications.
The main takeaway here is that one should look at the pixel-size of the camera AND the optical resolution of the lens. The lens in our example that is specified to have 100 lp/mm optical resolution (and therefore not ideal for use with a 3.45μm pixel) would be well matched with a camera that has a limiting pixel-size of 500/100lp/mm [pixel size ≤ 5μm]. In this case, a 200 lp/mm lens would be overkill. This also means that the 100 lp/mm lens in our previous example would be well matched to a camera that had, for example, 5.5μm pixels.
Doesn’t Diffraction play a role?
It is worth noting that camera+lens systems are typically not diffraction-limited in their optical resolution except when the lens-iris is set to a very small aperture (corresponding to a large f/#, typically higher than f/8). The optical resolution of a camera+lens system is likely to be limited by the optical quality of the lens (specified in line pairs per mm) or by the size of the pixels in the camera.
This is shown in the table below. The Numerical Aperture is calculated using the formula NA = 1/(2*f/#). The diffraction limited resolution is estimated at a wavelength of 550nm, using the Rayleigh Criterion:
Diffraction limited spot size = 0.61*lambda/NA
From the above, one can derive the Diffraction limited resolution in lp/mm by calculating: 500/Diffraction limited spot size (in μm)
If we assume that the manufacturer’s specification for the optical quality at the center of the lens is 100 lp/mm, the overall optical resolution is limited by the optical quality of the glass (100 lp/mm) or the camera pixel size (unspecified in this example) except for aperture settings f/8, f/11 and f/16 at which the system will be diffraction-limited to 89, 75 or 45 lp/mm.
F/# and diffraction-limited resolution
| f/# | NA | Diffraction limited resolution (@550nm) in μm | Diffraction limited resolution (in lp/mm) | Optical Resolution of Glass ≈ 100 lp/mm | System Resolution (lp/mm) |
| 1.4 | 0.36 | 0.93 | 538 | 100 | 100 |
| 2 | 0.25 | 1.34 | 373 | 100 | 100 |
| 2.8 | 0.18 | 1.86 | 269 | 100 | 100 |
| 4 | 0.13 | 2.58 | 194 | 100 | 100 |
| 5.6 | 0.09 | 3.73 | 134 | 100 | 100 |
| 8 | 0.06 | 5.59 | 89 | 100 | 89 |
| 11 | 0.05 | 6.71 | 75 | 100 | 75 |
| 16 | 0.03 | 11.18 | 45 | 100 | 45 |
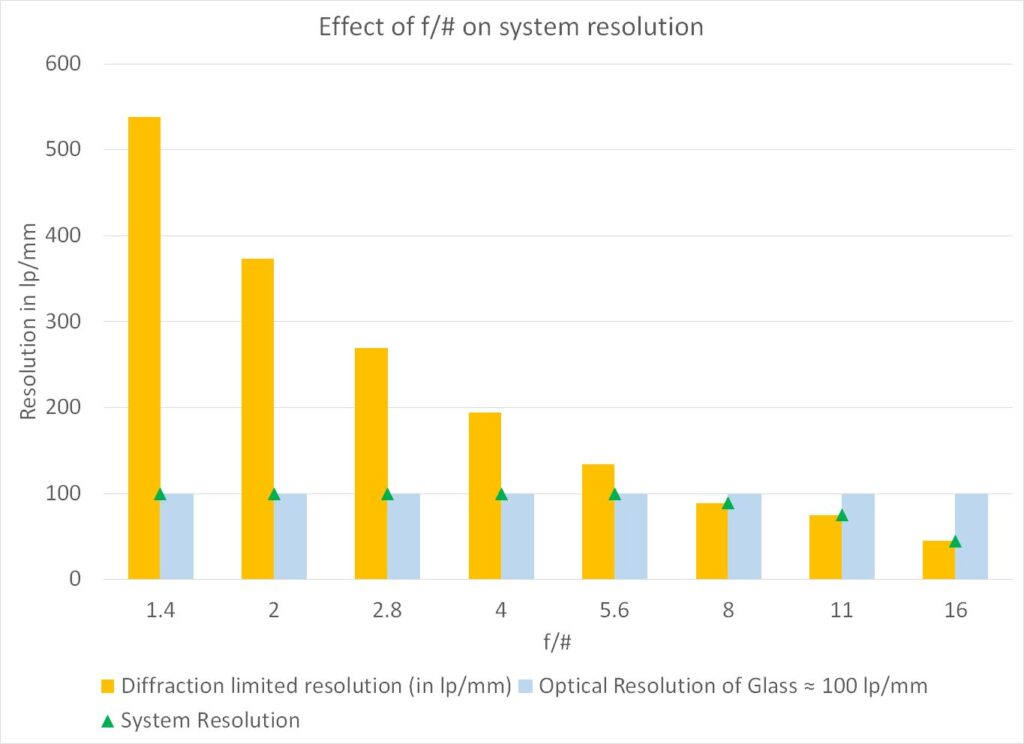
The main takeaway is that the effect of diffraction on the optical resolution of a camera+lens system can usually be ignored for use-cases in which the iris of the lens is NOT stopped down, i.e. the lens-iris is set to a relatively low f/#. There are, however, use-cases in which the iris of a lens is “stopped down”, i.e. set to a high f/#. This is often done to increase the Depth of Field (DOF), therefore it is not uncommon to see the image “softening” perceptibly as the lens-iris is stopped down to improve DOF.
Bringing it all together
Having looked at the effects of pixel-size, optical-quality and diffraction (f/#), we can draw the following inference. The limiting optical resolution of the system [in lp/mm] is based on whichever one of these three is the lowest. The following illustrative examples show how this information can be used to estimate the optical resolution of the system under different conditions.
Case 1: pixel size = 3.45μm | Optical quality of lens = 160 lp/mm
| f/# | Diffraction limited resolution (in lp/mm) | Limiting Resolution (in lp/mm) for a pixel size of 3.45μm | Optical Resolution of Glass ≈ 160 lp/mm | System Resolution (lp/mm) |
|---|---|---|---|---|
| 1.4 | 538 | 145 | 160 | 145 |
| 2 | 373 | 145 | 160 | 145 |
| 2.8 | 269 | 145 | 160 | 145 |
| 4 | 194 | 145 | 160 | 145 |
| 5.6 | 134 | 145 | 160 | 134 |
| 8 | 89 | 145 | 160 | 89 |
| 11 | 75 | 145 | 160 | 75 |
| 16 | 45 | 145 | 160 | 45 |
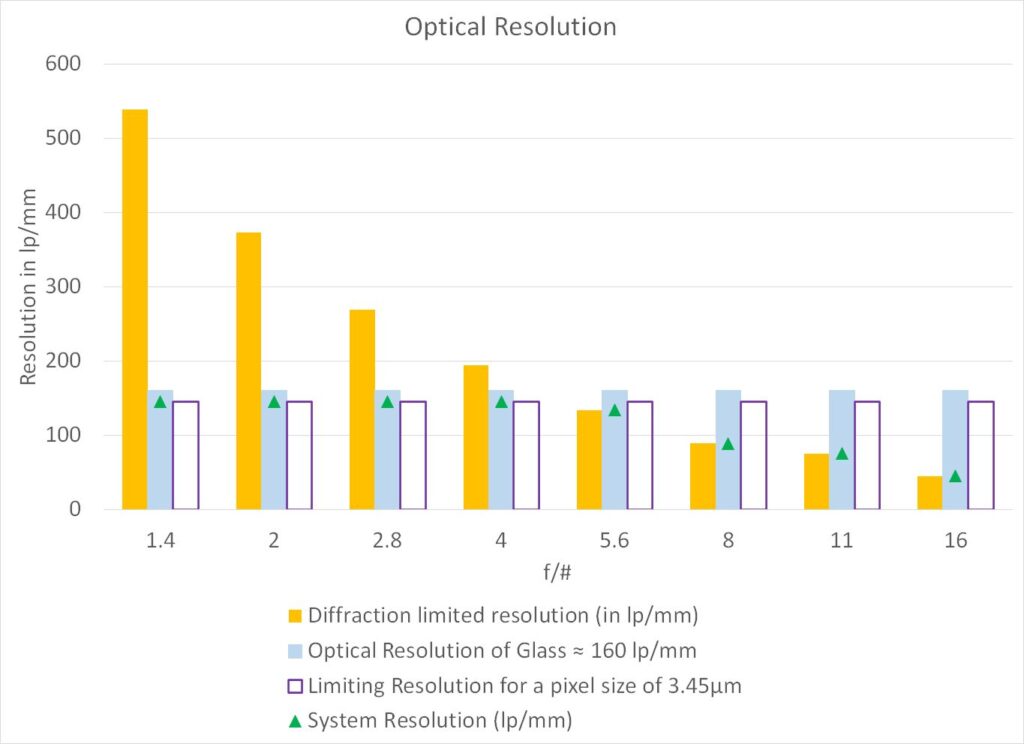
The optical resolution of the system in Case 1 is limited by the pixel-size of the camera at lower f/#s and it is diffraction-limited at higher f/#s.
Case 2: pixel size = 2.4μm | Optical quality of lens = 160 lp/mm
| f/# | Diffraction limited resolution (in lp/mm) | Limiting Resolution (in lp/mm) for a pixel size of 2.4μm | Optical Resolution of Glass ≈ 160 lp/mm | System Resolution (lp/mm) |
|---|---|---|---|---|
| 1.4 | 538 | 208 | 160 | 160 |
| 2 | 373 | 208 | 160 | 160 |
| 2.8 | 269 | 208 | 160 | 160 |
| 4 | 194 | 208 | 160 | 160 |
| 5.6 | 134 | 208 | 160 | 134 |
| 8 | 89 | 208 | 160 | 89 |
| 11 | 75 | 208 | 160 | 75 |
| 16 | 45 | 208 | 160 | 45 |
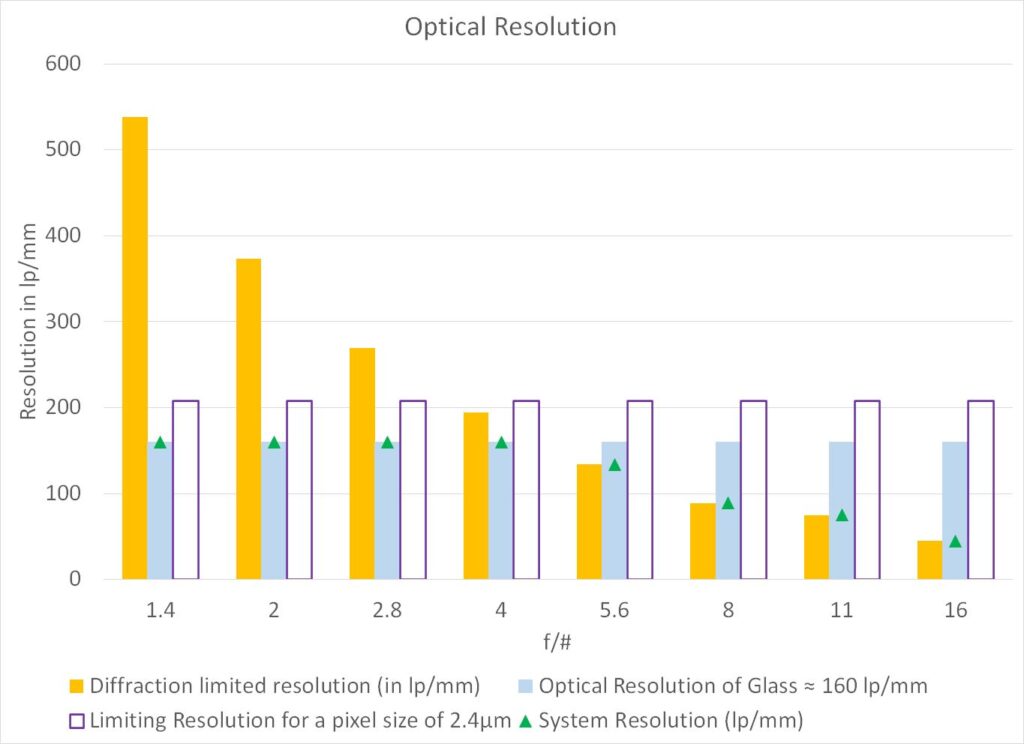
The optical resolution of the system in Case 2 is limited by the optical quality of the lens at lower f/#s and it is diffraction-limited at higher f/#s.
Case 3: pixel size = 2.4μm | Optical quality of lens = 220 lp/mm
| f/# | Diffraction limited resolution (in lp/mm) | Limiting Resolution (in lp/mm) for a pixel size of 2.4μm | Optical Resolution of Glass ≈ 220 lp/mm | System Resolution (lp/mm) |
|---|---|---|---|---|
| 1.4 | 538 | 208 | 220 | 208 |
| 2 | 373 | 208 | 220 | 208 |
| 2.8 | 269 | 208 | 220 | 208 |
| 4 | 194 | 208 | 220 | 194 |
| 5.6 | 134 | 208 | 220 | 134 |
| 8 | 89 | 208 | 220 | 89 |
| 11 | 75 | 208 | 220 | 75 |
| 16 | 45 | 208 | 220 | 45 |
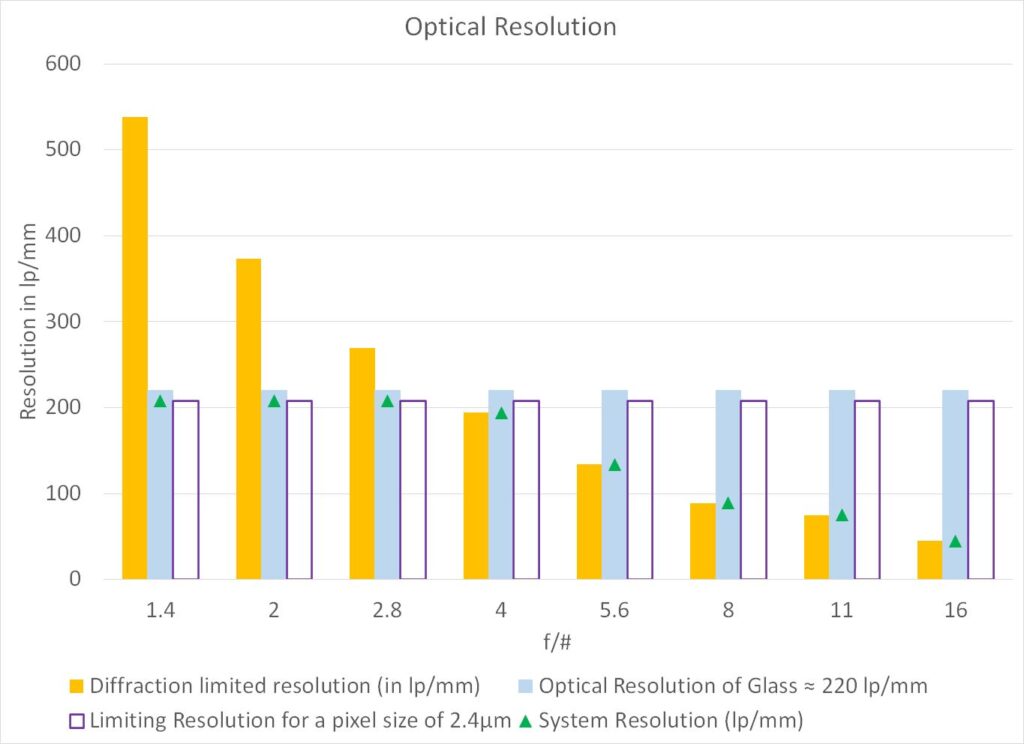
The optical resolution of the system in Case 3 is limited by the pixel-size of the camera at lower f/#s and it is diffraction-limited at higher f/#s.

