Definition of f/#
The f/# setting on a lens controls many of the lens’s parameters: overall light throughput, depth of field, and the ability to produce contrast at a given resolution. It is a measure of how efficiently light passes through the lens, and is a function of the aperture diameter as well as the focal length. Lenses with lower f/#s allow more light to pass through the system, while lenses of higher f/#s are considered slow and feature reduced light throughput.
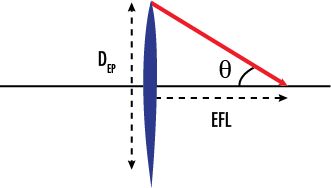
The f/# of a lens is defined as the ratio of its effective focal length (EFL) to its effective aperture diameter (DEP):
(1) f/#=EFL/ DEP {this defines the f/# at WD = infinity, at which the magnification is zero. When the WD is not infinity, a correction factor of (1+m) must be applied to the f/#, where “m” is the magnification: f/WD}
Adjusting the iris ring, changing the f/#
In most lenses, the f/# is set by the turning the iris adjusting ring, thereby opening and closing the iris diaphragm inside. The numbers labeling the ring denote light throughput with its associated aperture diameter. The numbers usually increase by multiples of √2. Increasing the f/# by a factor of √2 will halve the area of the aperture, effectively decreasing the light throughput of the lens by a factor of 2.
Lens iris-setting and light collection
The table below shows an example of f/#, aperture diameters, and effective opening area for a 25mm focal length lens with a maximum aperture of f/1.4. Notice that from the setting of f/1.4 to f/2.8, and again for f/4 to f/8, the lens aperture is reduced by half and the effective area is reduced by a factor of 4 at each interval. This illustrates the reduction in throughput associated with increasing a lens’s f/#.
| f/# | Lens Aperture Diameter (mm) | Aperture Opening Area (sq-mm) |
| 1.4 | 17.9 | 250.5 |
| 2 | 12.5 | 122.8 |
| 2.8 | 8.9 | 62.6 |
| 4 | 6.3 | 30.7 |
| 5.6 | 4.5 | 15.7 |
| 8 | 3.1 | 7.5 |
In the next table, similar information is provided about a DO-5095 (50mm, f/0.95 lens). It is immediately obvious that this lens has a much wider aperture area and therefore the light collection of this lens will be significantly better than the lens in the previous table.
| f/# | Lens Aperture Diameter (mm) | Aperture Opening Area (sq-mm) |
| 0.95 | 52.6 | 2176.5 |
| 1.4 | 35.7 | 1002.2 |
| 2 | 25.0 | 491.1 |
| 2.8 | 17.9 | 250.5 |
| 4 | 12.5 | 122.8 |
| 5.6 | 8.9 | 62.6 |
| 8 | 6.3 | 30.7 |
| 11 | 4.5 | 16.2 |
| 16 | 3.1 | 7.7 |
What are Fast Lenses?
One can take an image of equivalent brightness at a shorter camera exposure with a lens that has a lower f/# than with a lens that has a higher f/ (all else being the same). Lenses with low f/# numbers are therefore referred to as fast lenses, and they are a good choice for low-light applications, The above table shows the aperture and area estimates for the DO-5095. This is a lens from a family of fast lenses that includes the DO-1795, DO-2595 and DO-5095 with f/0.95 and with focal lengths of 17mm, 25mm and 50mm respectively. From the Aperture Opening Areas shown in the above tables, one can infer that fast lenses contain much more optical-quality glass, and this leads to their commensurately higher cost.
f/# and Depth of Field
The f/# impacts more than just light throughput. Specifically, f/# is directly related to the theoretical resolution and contrast limits and the Depth of Field (DOF) and depth of focus of the lens. Additionally, it will influence the aberrations of a specific lens design.

As pixels continue to decrease in size, f/# becomes one of the most important limiting factors of a system’s performance because its effects on DOF and resolution move in opposite directions. These requirements are often in direct conflict and the system designer typically accepts a compromise that makes sense for a particular application.
f/# and Numerical Aperture (NA)
It can be useful to visualize the overall light throughput of a lens in terms of the cone angle. Numerical Aperture – a term that is familiar to microscope users – applies to camera lenses as well. In fact, an infinity-corrected microscope objective can be thought of as a camera lens that is focused at infinity and used in reverse!
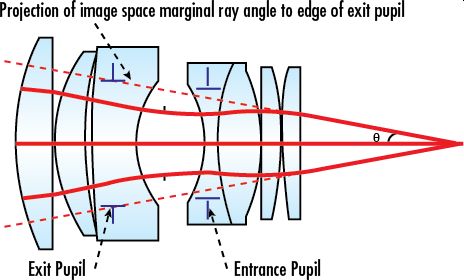
As in a microscope objective, the numerical aperture (NA) of a lens is defined as the sine of the marginal ray angle. However, in lenses it is defined in image space, unlike in microscope objectives for which it is defined in object space.

The f/# and NA are inversely related:
NA=1/2⋅(f/#)
An f/# of 1.4 thus corresponds to a Numerical Aperture of 0.36, and an f/# of 0.95 corresponds to a Numerical Aperture of 0.53, a relatively high number. This is shown on a table in the next topic on this thread, titled “Optical Resolution”.

