Spectral Responsivity
As introduced in the previous article titled “Quantum Efficiency and Spectral Responsivity“: Spectral responsivity is an estimate of the number of photoelectrons that are generated by a unit of radiant energy (1 nJ/cm2). It conveys similar information as the Quantum Efficiency, but allows us to conceptualize the conversion of light to photoelectrons in radiometric units. This can be useful, for example, in estimating the response of a camera to laser illumination at different energy levels and/or wavelength.
This article details the method of estimating Spectral Responsivity of an imager, if its Quantum efficiency is known. Please visit our other Knowledge Base article for definitions and descriptions of these terms, as well as for estimated Spectral Responsivity and Quantum Efficiency curves for sCMOS and CMOS imagers (one of which is shown here as an example).
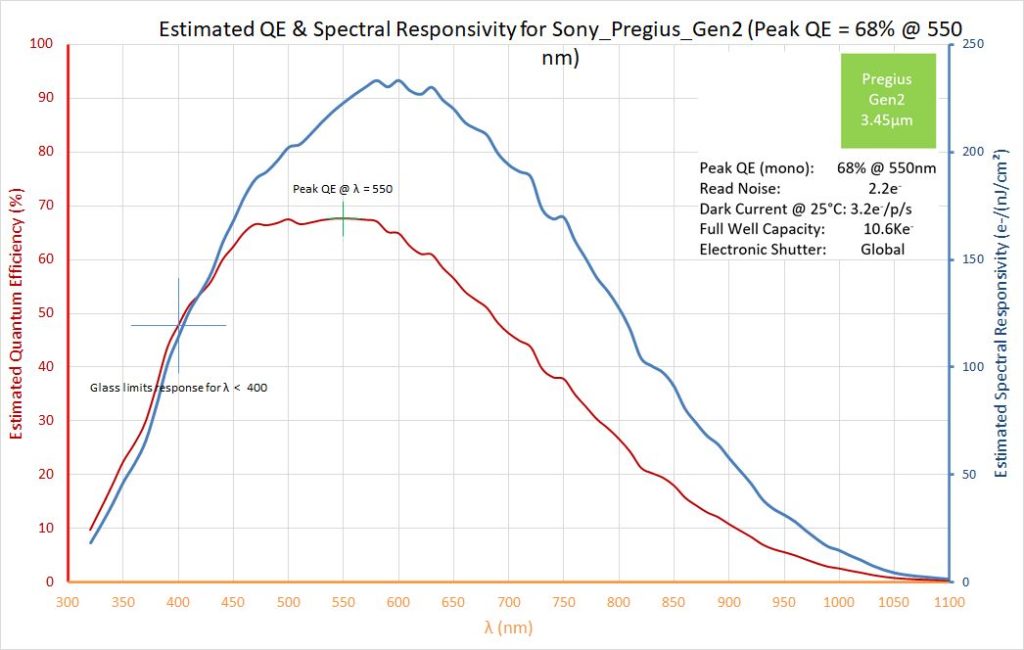
Spectral Responsivity may be estimated if Quantum Efficiency data is available. The first step is to calculate the energy (in eV) per photon for a given wavelength λ (nm), recognizing that there is an inverse relationship governed by Planck’s equation. This was introduced and shown graphically in the previous article titled “Quantum Efficiency and Spectral Responsivity“.
For example, at λ = 500nm: the energy per photon = 1239/λ = 2.48 eV (1)
We then compute how much energy (in eV) is incident on each pixel per 1nJ/cm2, given that:
1eV is 1.602 x 10-10 nanojoules (nJ) => 1nJ/cm2 = 0.624 x 1010 eV/cm2
The energy/pixel is obtained by multiplying by the pixel area for a given imager. For example, for pixels that are 3.45μm x 3.45μm, we get:
Energy/pixel (per 1nJ/cm2) = 0.624 x 1010 eV/cm2 x 11.9 x 10-8 = 7.43 x 102 eV (2)
Combining (1) and (2) we get the number of photons/pixel that represent a radiant energy of pixel_area x 1nJ/cm2 at a particular wavelength. For λ = 500nm, it is 7.43 x 102 eV divided by 2.48 eV = 300 photons.
We now multiply this number (300 photons) by the Quantum Efficiency at λ = 500nm and this gives us an estimate for the e/(nJ/cm2). If the QE at λ = 500nm is 67%, this yields 201 e/(nJ/cm2) at λ = 500nm. A similar calculation can be performed at all the wavelengths for which the QE is known, and the results can be shown in a Spectral Responsivity in e/(nJ/cm2) vs wavelength graph.
Note: If the gain of the camera is known (in e/ADU: electrons per Analog-to-Digital Units) then one could simply scale the graph to arrive at a graphical representation in terms of ADU/(nJ/cm2) vs. wavelength.

