Dr. Kurt Thorn (UCSF) begins this iBiology video with a historical summary of the work of Ernst Abbe (1840-1905) who formalized the definition of resolution in 1873 after conducting a groundbreaking experiment, referred to as the Abbe Diffraction experiment. Dr. Thorn describes the experiment in which a sample, which is theoretically represented as a diffraction grating with a repeating pattern of dark and light lines that are close together. Beginning at about the 7:00 mark Dr. Thorn conducts a must-see experiment, in which a microscope is configured from optical components and laid out on a light table. He uses a beam-splitter and two cameras to show (alternately) the image formed by the tube lens and the image at the back focal plane – the Fourier plane – of the objective. In doing the experiment with different samples and then by showing the effect of simple filtering in the Fourier plane, he concretizes the above abstract concepts in the mind of the viewer.
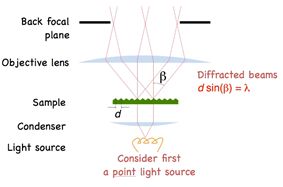
Applying Bragg’s law we arrive at the diffraction angle being determined by the equation dSin(β) = λ, where d is spacing of the diffraction grating, β is the angle of diffraction and λ is the wavelength of light. For a finer diffraction pattern, the diffraction angle increases – and if the angle is greater than α, the maximum angle that can be collected by the objective, then no information will be captured about the stripes. All that we would see is the 0th order transmitted light through the sample. What this means is that if β > α then no image is formed.
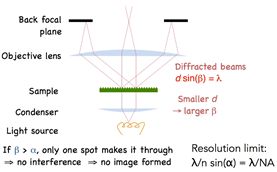
The limiting case may be obtained by setting the diffraction angle equal to the largest angle that can be collected by the objective. From this, Abbe was able to deduce the resolution limit of a microscope as governed by the equation dSin(α) = λ. The refractive index “n” is applied to account for different media, and the resolution limit is improved by an additional factor of 2 because we are not limited to the on-axis illumination, but there is a full range of angles to illuminate the sample.
Another insight is that diffraction in the sample tells us something about the size of the objects in the field of view and interference between the diffracted beams is what gives rise to the image of the sample. Dr. Thorn conveys this insight in the form of a famous quote from Abbe: “The microscope image is the interference effect of a diffraction phenomenon”.
In this iBiology video, Prof. Jeff Lichtman (Harvard University) describes the phenomenon of diffraction, a critically important concept because it is diffraction that limits the optical resolution of Light Microscopes.
Building on the concept of diffraction that was described in the previous iBiology video, Prof. Jeff Lichtman (Harvard University) explains that for a point object on the focal plane (such as an infinitesimally small fluorescent bead) the Point Spread Function (PSF) is the resulting distribution of light at and near the image plane. He further explains the influence of the previously described concept of Numerical Aperture on the PSF, and how this relates to optical resolution.
In this iBiology lecture Prof. Lichtman leverages the previously explained concepts of diffraction, NA and PSF and builds up to the final payoff: optical resolution. How close could two points be in the sample plane and still be resolved as separate points in the image. We learn about the Rayleigh Criterion, and that it is different for the XY and XZ planes of a microscope. Our main takeaway is that the higher the NA, the smaller the Rayleigh Criterion and the better the resolution. Prof. Lichtman then shows a sequence of images taken with cameras that have different pixel pitches providing a visual insight into why the sampling in the image plane must be sufficient to resolve an image. This can be quantified by applying the Nyquist Criterion to the spatial sampling on the image plane, leading to an upper limit on the pixel size of the image sensor that is used in conjunction with a microscope.
In the following table, “R” represents the Rayleigh Criterion for the diffraction-limited spot size: R = 1.22λ/(2NA)
| Objective | R @550nm | On imager plane | Max pixel size (Nyquist limit) |
| 40X/0.75NA | 0.45µm | 0.45 x 40 = 18µm | 9µm |
| 4X/0.13NA | 2.58µm | 2.58 x 4 = 10.32µm | 5.16µm |
The above method can be used to estimate the performance of a camera and a microscope system, as long as the relevant parameters of the camera and the microscope objective are known. In the table below, we show the Limiting Resolution (in µm) and the Field of View for several commercially available microscope objectives when used with a 2048 x 2048 camera with 6.5µm pixels: this includes non-cooled sCMOS cameras such as the pco.panda 4.2, pco.panda 4.2bi and the pco.panda 4.2bi uv. This table also applies to cooled sCMOS cameras such as the pco.edge 4.2, pco.edge 4.2bi and pco.edge 4.2bi uv cameras.
| Camera Parameters | ||||||||
| Optical Format | #Megapixels | #H pixels | #V pixels | Pixel size (μm) | H size (mm) | V size (mm) | Diagonal (mm) | |
| 18.8mm < 4/3" | 4.2 | 2048 | 2048 | 6.5 | 13.31 | 13.31 | 18.83 | |
| Commercially Available Objectives | ||||||||
| Objective: Mag/NA | 1X\0.03NA | 2X\0.1NA | 4X\0.13NA | 10X\0.26NA | 20X\0.5NA | 40X\0.75NA | 60X\0.85NA | 100X\1.4NA |
| Min. feature size (um) | 11.18 | 3.36 | 2.58 | 1.29 | 0.67 | 0.45 | 0.39 | 0.24 |
| Max pix size (um) | 5.59 | 3.36 | 5.16 | 6.45 | 6.70 | 9.00 | 11.70 | 12.00 |
| FN (mm) | 22 | 22 | 22 | 22 | 22 | 22 | 22 | 22 |
| WD (mm) | 8 | 56.3 | 17.2 | 16 | 2.1 | 16 | 0.66 | 0.31-0.4 |
| NA | 0.03 | 0.1 | 0.13 | 0.26 | 0.5 | 0.75 | 0.85 | 1.4 |
| Magnification | 1 | 2 | 4 | 10 | 20 | 40 | 60 | 100 |
| Estimated Performance of Camera and Objective Combinations | ||||||||
| (*) Limiting Resolution (µm) | 13 | 6.5 | 3.25 | 1.3 | 0.67 | 0.45 | 0.39 | 0.24 |
| Vignetting? | No | No | No | No | No | No | No | No |
| FOV (H x V) mm | 13.31 x 13.31 | 6.66 x 6.66 | 3.33 x 3.33 | 1.33 x 1.33 | 0.67 x 0.67 | 0.33 x 0.33 | 0.22 x 0.22 | 0.13 x 0.13 |
| FOV (diagonal) mm | 18.83 | 9.42 | 4.71 | 1.88 | 0.94 | 0.47 | 0.31 | 0.19 |
| Please contact our imaging experts for assistance in selecting a camera & objective combination that fulfils your FOV & resolution requirements at application-specific wavelengths. | ||||||||
| 1) The minimum feature size is estimated using the Rayleigh Criteria at λ = 550nm; it can be re-calculated for other wavelengths. R = 1.22*λ/(2NA) | ||||||||
| 2) The maximum pixel size is estimated by applying the Nyquist criteria to the minimum feature size as it appears on the imager plane. Maximum pixel size = R*magnification/2 | ||||||||
| 3) Camera and Objective combinations which meet the Nyquist criteria and are therefore diffraction limited are indicated by showing the Limiting Resolution in green font. (*) | ||||||||
| 4) Values for Working Distance (WD) and Field Number (FN) are shown for reference only. Actual values may vary. | ||||||||
| 5) Vignetting, a darkening of the image at the corners, may be observed if the Imager Diagonal is larger than the Field Number of the Objective. | ||||||||
Dr. Jennifer Waters (Director of the Nikon Imaging Center, Harvard Medical School) provides additional insight on the topic of Numerical Aperture (NA). Numerical Aperture is critical because it limits both the resolution and the brightness of an image obtained from a microscope. She begins with the Rayleigh Criteria, showing how NA impacts resolution and then shows the physical properties that impact NA. This leads into an informative discussion about the benefits of higher NA.
The Point Spread Function (PSF) of microscope is the basis for many practical and theoretical concepts in light microscopy, both basic and advanced. In the video, Dr. Jennifer Waters defines the PSF of a microscope and then shows how it relates to the resolution of a microscope. She further explains that the PSF is a result of diffraction and interference: this concept is concretized in the video with the help of animations and examples. This video is also very helpful in integrating in the viewer’s mind the concept of the PSF with the well-known Rayleigh Criterion. Dr. Waters also helps viewers connect the PSF to real-world insights: for example, (citing Vogel et al, Science, 2006) one can fit ~3million GFP molecules into the PSF maxima of a typical high NA objective!
She likens the process of convolving each point source in the sample with the PSF as “stamping a PSF on every point-source in the sample”. The analogy she uses is of the PSF being like a paint brush of a particular size, used to create an optical image from all the point sources in an image. For this reason, objects in a diffraction limited image of a sample will never appear smaller than the PSF. This is shown clearly in both animated images and real-world examples of fluorescence microscopy images.
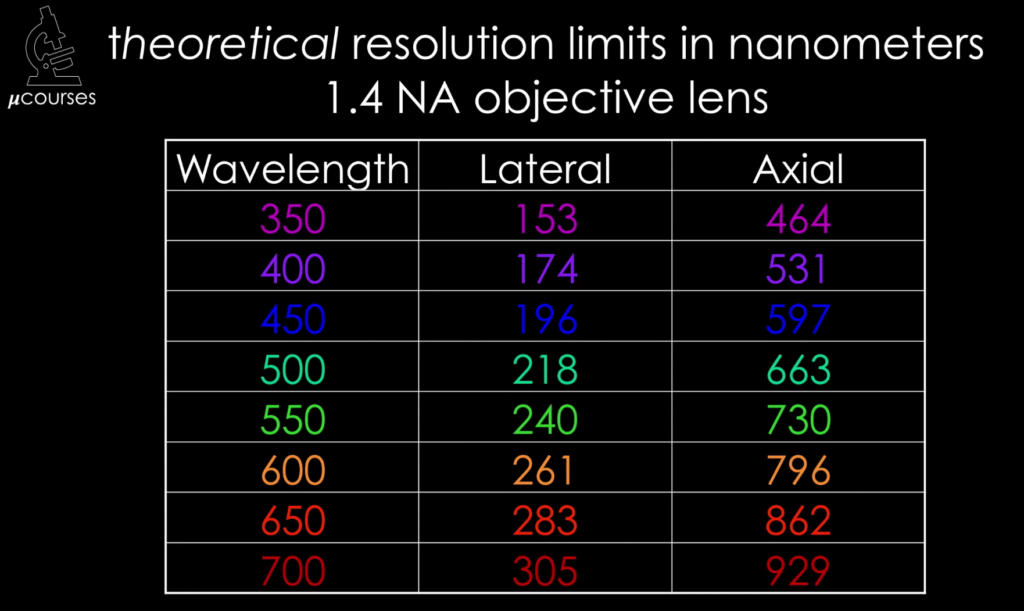
In this iBiology video, Dr. Bo Huang (UCSF) explains the concept of a Fourier transform, and links it to the operation of the objective of a microscope. He shows how the back focal plane of an objective provides a Fourier transform and uses this information to derive the equation for the diffraction limit.

