Using SNR as a Figure-of-Merit
The Signal-to-Noise Ratio (SNR) is simply the Signal divided by the Total Noise in a system: it is a convenient figure-of-merit to evaluate how well the signal overcomes the noise in the system under a particular set of conditions. It provides a way to quantitatively compare images, because a higher SNR usually correlates with an observable improvement in image quality. For applications in which an image is a source of data that is analyzed by image processing algorithms, a higher SNR can be a critical requirement because it improves the accuracy and repeatability of the process. An image with a higher SNR permits a finer quantization of data which can be important in detecting small differences in the grayscale values within an image, or between multiple images. For inspection and detection applications in which an image is used to discern or quantify features that are difficult to see, a higher SNR can improve the detection threshold.
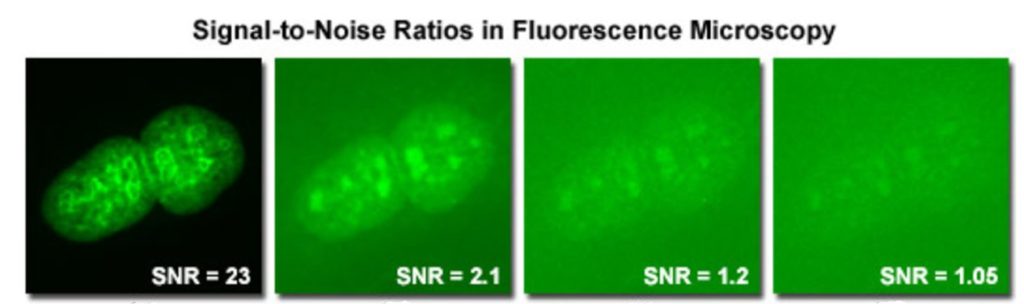
In low-light applications such as fluorescence microscope imaging, the SNR achieved by a camera is critical because of the inherently low light conditions. In such applications, the camera must generate a signal that is large enough to overcome the overall noise in order to obtain a discernible image with an acceptable Signal-to-Noise Ratio (SNR). {the images above demonstrate LOW/HIGH SNR imaging}.
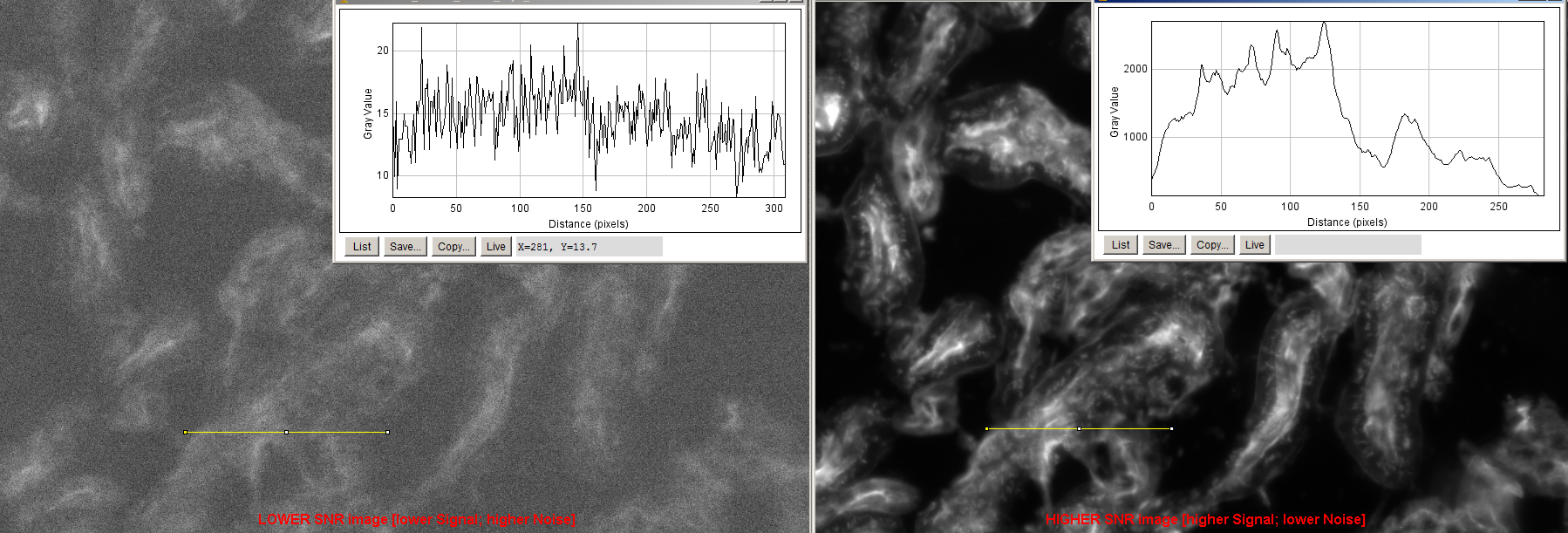
From the above images, we can see how SNR is useful as a figure of merit when comparing the image quality of two images. This points to its use as a method of quantitatively evaluating an imaging system under different conditions, e.g. under different exposure settings, or perhaps under different illumination conditions. We can estimate the SNR in each case and then evaluate other tradeoffs, such as the time taken for each exposure – which affects the overall throughput of our workflow. Or, having estimated the different SNRs under different illumination conditions, we can observe the tradeoffs with respect to the effect of increasing the brightness of the light source on our samples, or of the cost of the system. This allows us to make informed decisions in our Design of Experiments – by examining the tradeoffs, we may arrive at a combination of parameters, such as the brightness of a light source, the exposure setting of a camera that optimizes SNR. While doing so, we may also be required to consider the effect of bright light on the longevity of fragile samples and/or the effects of photobleaching in applications such as fluorescence microscopy.
In a similar manner, SNR can be useful as a figure-of-merit for image quality in comparing two or more different imaging systems under similar conditions. This method is applicable to the selection of components. In fact, one can use the estimated SNR under typical conditions of an experiment to identify the camera technology that is most suitable for acquiring quantitatively useful images.
Estimating SNR
SNR is simply the Signal, divided by the Total Noise. We can estimate the value of the Signal (in electrons) in terms of camera parameters such as its Quantum Efficiency and camera settings such as the Duration of Exposure.
S (in electrons) = P * QE * t ———————– [Equation #1]
P = the light level, represented by the Photon Flux in photons/pixel/sec. Defining “P” in these units carries with it an implicit assumption that the same number of Photons fall on each pixel of the different cameras being compared, even if the pixels of different cameras happened to be of different sizes. This doesn’t represent a typical experiment, in which the optics remain the same, while cameras with different pixel sizes are swapped in and out for evaluation. Note that we could model this type of experiment by simply choosing different unit for “P”: if we wanted to take the pixel dimensions of different cameras into consideration, we could use P to represent photons/sq-um/sec instead of photons/pixel/sec. In this case, the estimated signal (in electrons) would be S = P * a * QE * t, where “a” is the area of a pixel, easily estimated from the pixel dimensions that can be obtained from the datasheet of a camera.
QE = the Quantum Efficiency (QE, the probability of photons being converted into electrons, expressed as a % and having a significant dependence on the wavelength of incident light)
t = duration of exposure (seconds)
Estimating the Total Noise in an imaging system is somewhat more complex, since we have to account for all the sources of noise: Photon Shot Noise, Read Noise & Dark Shot Noise. There are a few other sources of noise that were not described in the previous section, for example, Fixed Pattern Noise – which is an estimate of the spatial non-uniformities across the imaging area. Fixed Pattern Noise is typically quite low in scientific grade cameras, and can be considered negligible for the purposes of this discussion. We also have to consider the manner in which the noise components are to be added.
Photon shot noise, the statistical temporal variability in the number of photo-electrons that are collected by a pixel during exposure. This is the statistical noise associated with the arrival of photons at the pixel. Since photon arrival obeys Poisson statistics, it is reasonable to estimate a Poisson distribution in the #Signal_electrons. Therefore, Photon shot noise can be estimated to be the Sqrt(P*QE*t).
Read Noise (Nr, in electrons) of an imager: This depends on the choice of the imaging technology, for example sCMOS image sensors typically have a low read noise as compared with most CCD or CMOS cameras. Read Noise also depends very significantly on the camera design techniques. In cameras that are designed for use in low-light scientific imaging applications, everything, from size/enclosure design to circuit board layout is done with the goal of minimizing noise, with read noise being a primary concern. In cameras that are designed for use in less stringent bright-light applications, a camera designer may focus, for example, on reducing the size/cost of the camera while permitting some tradeoffs in read noise.
Dark shot noise, the statistical temporal variability in the number of thermal-electrons that are collected by a pixel during exposure. The #dark electrons is estimated to be the product of dark current and the duration of exposure. It is reasonable to assume a Poisson distribution, therefore dark shot noise can be estimated to be the sqrt[Dark current (in electrons/pixel/sec) * exposure (in sec)].
Dark current (Id, in electrons/pixel/sec): a flow of thermally generated electrons, which doubles for every ~7°C rise in temperature. Thermally generated electrons flow even when there is no light and may be referred to as “dark electrons” or “leakage electrons”. Their number can be estimated as Id*t electrons for each pixel, collected during an exposure of t sec. They cannot be distinguished from photon-generated electrons, and the temporal variability in the number of dark electrons is referred to as dark-shot-noise. The number of dark electrons accumulated in a pixel over time (Id*t) follows a Poisson distribution, and therefore dark-shot-noise can be estimated as Sqrt(Id*t) electrons. It is negligible for imaging under bright light conditions because the duration of exposure typically a few milliseconds. However, it can be a significant factor when the duration of exposure exceeds 3~5 seconds. Cooling the imager reduces the value of Id (as stated above, Id doubles for every ~7°C rise in temperature).
Note: uncorrelated noise sources add in quadrature. Fixed pattern noise is ignored for this calculation since it is assumed to be negligible for the “scientific” class of image sensors.
Total Noise = Sqrt(Photon_shot_noise2 + Read_noise2 + Dark_shot_noise2)
Noise = Sqrt(P*QE*t + Nr2 + Id*t) ——————— [Equation #2]
Since SNR = Signal/Noise, we can estimate SNR by simply dividing Equation #1 by Equation #2.
SNR = P*QE*t/ Sqrt(P*QE*t + Nr2 + Id*t) ——————– [Equation #3]
The above equations are the basis for the quantitative and graphical analysis that is detailed in the next few topics.

